GPE Hamiltonian

Description

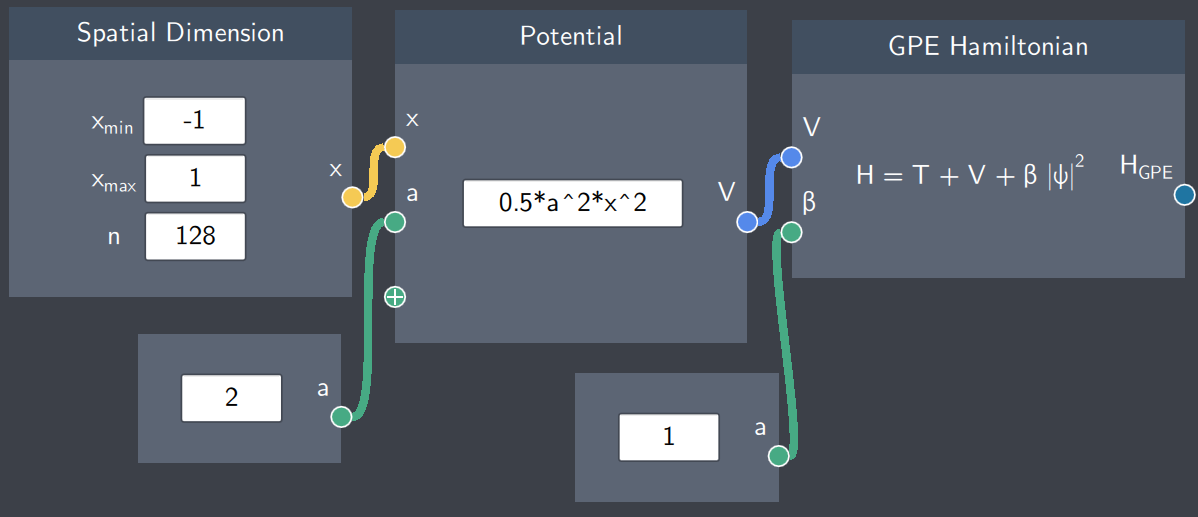
The GPE Hamiltonian node defines the total energy of the system modelled by the Gross-Pitaevskii equation describing the mean field of Bose-Einstein condensates. It is the first building block to get the energy spectrum of a system.

Inputs

The node has the following inputs: 

• Potental (V): A potential function defined in the Potential node 
• Self-interaction ($\beta$): A scalar quantity denoting the interaction strength of the condensate

Content

The content in the node shows what is being calculated. It is the sum of the kinetic and potential energy and a non-linear term describing the self-interaction strength.

Output

The node outputs the Hamiltonian based on the GPE

Example 

In the example below, the GPE Hamiltonian has a harmonic oscillator potential as the potential function and the self-interaction strength of the system is equal to 1.