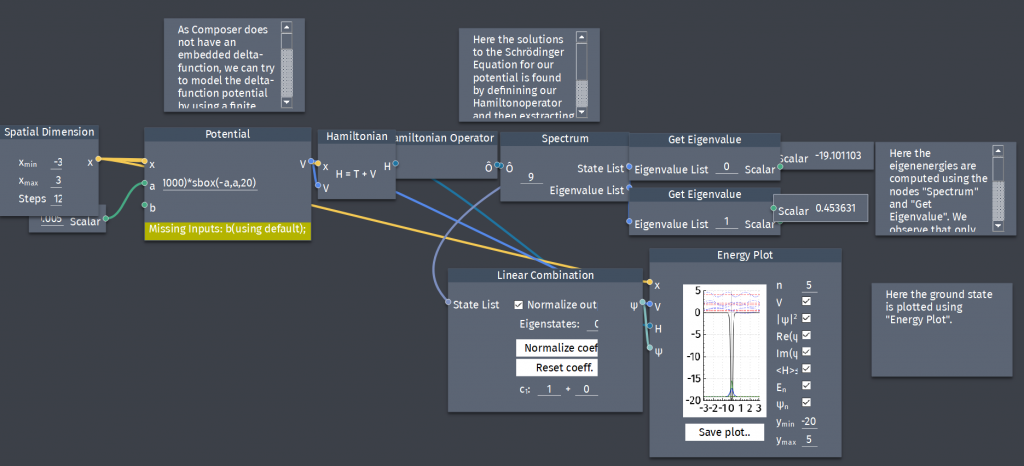
The delta-function potential approximated with a finite well
The Dirac-delta function can be thought of as the limiting case of a rectangle with area 1, as the height goes to infinity and the width goes to zero. Show that the delta-function well is a weak potential in the sense that $z_{0}=\frac{a}{\hbar}\sqrt{2mV_{0}}\rightarrow 0$ where $a$ and $V_{0}$ is the width and heigth of a finite square well respectively. Determine the bound state of the delta-function potential by treating it as the limit of a finite square well.